Artificially Evolving Intelligence
The Use of Biological Evolution as a Heuristic Method of Computation

The following is from a paper I wrote introducing the reader to genetic algorithms, along with associated ideas in computing such as the difficulty of solving NP-Complete problems. I assume the reader has no background and is written as clearly as possible.

Evolution, a theory explaining how simple biological systems can change into complex systems over time, is a scientific marvel. How could a single cell organism change into the vastly complicated human nervous system? How could we evolve our eyes, even though there are several interdependent structures needed for it to correctly function as a whole? This mystery has been frustrating biologists for centuries until Darwin, in his ground-breaking work “On the Origin of Species”, introduced the theory of evolution. This theory defines a process of small beneficial mutations that propagate to successive generations though natural selection, which may lead to better adaptation for a given environment.

The scientific community now accepts this theory as a valid explanation on the origins of biological systems, yet computer scientists are looking at evolution as a new powerful model of computation (Weise, Zapf, Geihs, 2007). Genetic algorithms, one of the most powerful type of heuristic algorithms, is an application of this theory. The power of genetic algorithms is that it may solve in part, or as a whole, the “Holy Grail” problem of all computer science: Artificial Intelligence (Negnevitsky, 2001). Our own intelligence seems to be out-growing the pace of our biological evolution. Many computer scientists agree that creating artificial human-like intelligence is a critically important topic of our own growing intelligence as a species. The notion that machine-intelligence outperforming human-intelligence is commonly called “the singularity”, with genetic algorithms being key to this event (Kushner, 2008).

Several common problems in computer science are fundamentally hard to solve, and are classified as “NP-complete”. “NP” stands for “nondeterministic polynomial time”, or more simply means that these types of problems have no known reasonably fast algorithmic solution, though testing a solution is easy. Most of these problems are currently solved through “brute-forcing”, which is a method of generating and testing all possible solutions. Even with modern computer hardware, and all of the world’s computers working in unison, it would take thousands or millions of years to solve problems within this classification, even if the input data size was small.

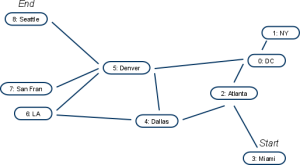
Examples of NP-complete problems include the famous “Travelling salesman problem”, in which a traveling salesman must choose the shortest path from one city to another, using a bus or train route, but knowing not all cities are directly connected (See Figure 1). Though there does not exist any formal solution, humans can easily accomplish this task as we subconsciously compute data in a fundamentally different way than how a computer would. We, as humans, make assumptions left and right until a solution “fits” in our minds for the given problem. We might make several assumptions, and change these assumptions while we solve the problem. Instead of testing all possible solutions, we narrow our solution space more and more until one correct path exists. Subconsciously, many mechanics are going on in our brain that we are not aware of. We might purge data that we do not think is relevant to the problem, as well as zoom in on a specific sub-problem or zoom out to observe the problem as a whole.

Since there is no formal solution to this problem, a computer must brute-force, testing every single possible solution until a correct solution is validated and known to be the shortest path. This is analogous to the computer having to try trillions of paths to find the cheapest path for the travelling salesman, possibly taking thousands of years to complete depending on the size and resolution of the map. To help computers overcome this, a class of algorithms work by trying to mimic what humans do with these kind of difficult problems: divide and conquer data, as well as simple guessing (IEEE, 2000). These are called heuristic algorithms, and like humans, heuristic algorithms are good at finding near-perfect solutions, but not necessarily the single perfect solution.

Figure 1: A sample series of interconnections representing city-to-city access for the United States. Distances can be defined through a table of connections. Note the starting and ending cities, in which the salesman is trying to move from and to as optimally as possible.

Many varying types of heuristic algorithms exist, but most attempt to solve a given problem through human-like methods. Some include “rule-based expert systems”, that follow attempts to make a statistical guess for the answer based on pre-programmed rules from an expert in the associated field. Neural networks, famous in the 1990’s, attempt to mimic basic neuron functionality within brains, but are too simple to represent a complex system, even by the thousands of neurons. Other similar systems exist, but only genetic algorithms have been shown to have special features that make it a powerful approach for difficult computing problems.

Genetic algorithms are named such because it uses the basic principles of evolutionary theory as a way to approach solving a problem. The problem’s solution is represented as a data structure, equivalent to a “gene”. Like a gene, the solution is encoded in a way such that segments may be merged, swapped, mutated, or have other operations applied, but remain mostly valid. Once this gene format is defined, a fitness function must also be defined that returns the correctness of the solution. Two different genes should have different “correctness” values, so that it is possible to quantify if one gene is “better” than another. This concept derives from the evolutionary concept of natural selection of an organism in its environment (Negnevitsky, 2001). If an organism is poorly adapted to its environment, it is said to have low fitness and is more likely to not reproduce. If it is able to survive and reproduce, it is said to have a high fitness, and thus have their good genes propagate.

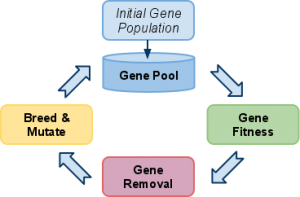
Once the gene structure and fitness functions are defined, a problem can be solved through a genetic algorithm simulation. A gene pool is created to represents an initial set of possible solutions. Depending on the problem at hand, the pool may start as completely randomized or set to an initial predefined set. Once the gene pool is filled, the simulation starts cycling through fitness measurements, poor-performing gene removal, high-performing gene reproduction, and finally mutations (See Figure 2).

Within this simulation we start by measuring the correctness of each gene, which is equivalent to measuring the correctness of a solution. Once we have all of the correctness values, we then cull the gene pool, which means removing genes from the pool that underperformed. This is up to the simulation’s rules and the associated needs from the problem definition. Sometimes, it is appropriate to remove a certain percentage of genes from the pool, or to remove only those that underperformed compared to a certain value. The initial culling is normally large, but as the genes converge towards a solution, more and more genes are found correct. The remaining genes are then allowed to reproduce, which is done by several methods of data combinatorics. Two or more “parent” genes are merged to create a new set of genes, such that gene segments may be swapped through different methods. Mutations are then introduced, introducing slight changes to allow variance in each potential solution. This is also useful in preventing homogeneous gene pools, which forces the simulation to cycle more often. The simulation is then repeated until a condition is met, defined by the simulation parameters. Most simulations usually end when the top-performing gene meets a certain correctness, defined by the simulation rules. Figure 2 demonstrates the simulation cycle.

Figure 2: This is a generic genetic algorithm simulation cycle, in which an initial pool has a set number of genes, which are then individually measured for correctness. Those that are considered “good” are kept for breeding, while “bad” genes are culled from the pool. Good genes then are reproduced by mixing their contents and have small mutations introduced at a set rate. The simulation is then repeated with the new gene pool.

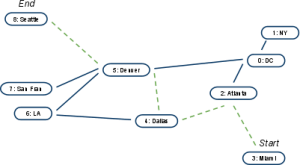
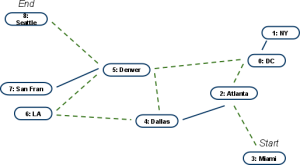
An applied example of genetic algorithms would be the “Traveling salesman problem”. A “gene” could be a set of adjacent indices to travel through (See Figure 3), and the initial gene pool could be filled with random paths. Gene fitness is simply the measurement of how long the path is from the starting to end positions. Combinations of genes, used for breeding, could be done by swapping chunks of the indices list, making sure to correct any small errors that might occur with new paths. Mutations could occur by introducing slight changes of the index numbers, but only to adjacent nodes to keep the data correct. Over time, a set of genes might emerge as the best possible paths to a target location, in which the simulation may stop if the path is shorter than a certain distance. The system may have to run over hundreds or thousands of simulation cycles, but is heavily dependent on how long the city list is.

Gene 1: City Indices 3, 2, 4, 5, 8

Gene 2: City Indices 3, 2, 0, 5, 4, 6, 5, 8

Figure 3: In this example, a traveling salesman “gene” is represented as a number of indices (cities) to move through, representing a single path a salesman may take. Gene 1 is more correct as it has a shorter distance to travel from the start to end, while the second gene has a longer path by repeating a city. The paths each gene takes is drawn in dashed green lines.